1. If (2a+1 )(2a+2)(2a+3)(2a+4)+q is a perfect square, then q

(A) 1 (B) 12 (C) 24 (D) - 8 

2. A block of cheese 5 cm by 6 cm by 8 cm is covered with wax Ifthe cheese is cut into one centimetre cubes, then number of cubes not having wax on them is

(A) 210 (B) 72 (C) 240 (D) 120

3. The radius of a wheel is 14 m. How many revolutions will it make in traveling 880 m?

(A) 14 (B) 10 (C) 12 (D) 16

4. The area of a circle is increased by 22 sq m. when its radius is increased by 1 m. Find the original radius of the circle. 

(A) 31A m (B) 3% m (C) 6 m (D) 3 m

5. Find the equation of a line parallel to y-axis and passing through the point (-3,4)

(A)  x - 4 = 0 (B) x + 4 = 0 (C) x - 3 = 0 (D) x +B = 0

6. If 69.5 is the mean of 72, 70, x, 62, 50, 71, 90, 64, 58 and 82, then the value of x is

(C) 72 (B) 76 (B) 75 (B) 67 

7.  A Rectangular lawn 80 m x 60 m has two roads each 10 m wide running in the middle of it. One parallel to the length and the other paralle! to the breadth. Find the cost of gravelling them at £20 per sq. m.

(A) 26,000 (B) 41,000 (C) 35,000 (D) 39,000

8. Let 

then which of the following relations is true? 

(A) y < z < x  (B) x > y >z  (C) x < y < z  (D) z < x < y 

9. The angles of a triangle are in arithmetic progression. If one of the angles is 75°, then the other two angles are 

(B) 65°, 85° (B) 60°, 90° (C) 46°, 60° (B) 55°, 65°

1.If a2 + b2 + c2 = ab + bc + ca, then which one is correct ?

(A) a + b + c = 0  (B) a = b = c     (C) a - b - c = 0  (D) None of the above

2.Ram and Shyam solve a quadratic equation. Ram makes a mistake in the constant term and finds the roots as 5, -3. Shyam makes a mistake in the co-efficient of x gets the roots as 1, -3. The correct roots are

(A) 1, 3  (B) -1, 3     (C) -1, -3      (D) 1, -1

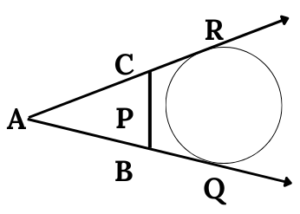
3. In the figure (not drawn to scale), a circle touches the side BC of △ABC at P and sides AB and AC produced at Q and R respectively. lf AQ = 10 cm, then the perimeter of △ABC is 

(A) 10 cm (B) 20 cm (C) 5 cm (D) 25 cm

4.If the semi perimeter of a right-angled triangle bes cm and hypotenuse be c cm, then the area of the triangle is

(A) s/ s-c cm    (B) sc sq.cm   (C) s(s - c) sq.cm    (D) None of the above

5.Three solid spheres of gold whose radii are 1 cm, 6 cm and 8 cm respectively are melted into a single solid sphere. Then the radius of the sphere is

(A) 7 cm       (B) 8 cm   (C) 9 cm              (D) 10 cm

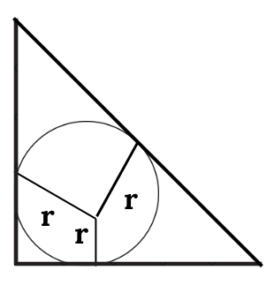
6.In the given figure, (not drawn to scale)

△ABC is a right angled triangle,

∠B=90o ∠B=90o, AB = 6 cm and BC = 8 cm, the value of r is

(A) 1 cm    (B) 2 cm         (C) 2.5 cm   (D) 3 cm

7.A right circular cone, a right circular cylinder and a hemisphere, all have the same radius and the heights of cone and cylinder equal their diameters. Then their volumes are proportional respectively to

(A) 2 : 1 : 3  (B) 1 : 3 : 1      (C) 1 : 2 : 3  (D) 3 : 2 : 1

8.In a triangle PQR, points A, B and C are the mid points of the sides PQ, QR and RP respectively. If the area of the.triangle ABC is 16 sq.units, then the area of the triangle PQR is

(A) 32 sq.unit           (B) 48 sq.unit           (C) 50 sq.unit  (D) None of the above

9.The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm from the centre, then the distance of the other chord from the centre is

(A) 5 cm       (B) 4 cm   (C) 3 cm          (D) 2 cm

10.A cylinder and a cone have equal radii of their bases and equal heights. If their curved surface areas are in the ratio 8 : 5, the ratio of radius to the height is

(A) 3 : 5   (B) 3 : 4   (C) 4 : 5       (D) 2 : 1

11.ABCD is a cyclic quadrilateral and the sides DC and AB, are produced to meet at P. If

∠APD=25o ∠APD=25o and ∠BPC=70o∠BPC=70o then ∠BAD ∠BAD is equal to

(A) 25°  (B) 70°  (C) 95°  (D) 85°

12.A hemispherical bowl is made of steel sheet 0.8 cm thick. The inside radius of the bowl is 5 cm. Volume of steel used in making it is

(A) 146 cm3     (B) 144.9 cm3   (C) 146.9 cm3     (D) 148.6 cm3

13.If P(1, 2), Q(4, 6), R(5, 7) and S(a, b) are the vertices of a parallelogram PORS, then the values of a and b are

(A) a = 2, b = 6        (B) a = 1, b = 5        (C) a = 2, b = 3   (D) a = 6, b = 7

14.The radius and height of a cone are each increased by 10%, then the volume of the cone is increased by

(A) 21%   (B) 33.1%   (C) 25.3%   (D) 30.4%

15.The areas of two similar triangles are 36 sq.cm and 81 sq.cm respectively. If the median of smaller triangle is 12 cm then the corresponding median of the larger triangle is

(A) 12 cm   (B) 18 cm      (C) 24 cm    (D) 10 cm

16. In the given figure, (not drawn to scale) △ABC is a right angled triangle, ∠B=90o , AB = 6 cm and BC = 8 cm, the value of r is 

(A) 1 cm (B) 2 cm (C) 2.5 cm (D) 3 cm

1.The area of a triangle is equal to the area of a square whose side measures 75 meters. Find the side of the triangle whose corresponding altitude is 125 meters.

(A) 70 m          (B) 75 m       (C) 90 m             (D) 65 

1.If a square and a rectangle having the same perimeter and their areas are S and R respectively then

(A) S = R      (B) S > R             (C) S < R         (D) None of the above

2.A parallelogram, a rectangle and triangular region stands on same base and between same parallel and if their area are P, R and T respectively, then

(A) P = R = 2T             (B) P = R = T/2  (C) 2P = 2R = T           (D) P = R = T

3.If x3 + 6x2 + 4x + K is divisible by (x + 2), then the value of K is

(A) - 6  (B) - 7     (C) - 8           (D) - 10

4.Which of the following geometric figure has diagonals equal in length ?

(A) Parallelogram        (B) Rhombus  (C) Trapezium      (D) Rectangle

5.A hemisphere can with internal radius of 9 cm is completely filled with water. Someone is requested to fill this water in a cylindrical bottle with a diameter of 3 cm and height of 4 cm. The number of bottles to be required to make the can empty is

(A) 54  (B) 128            (C) 36  (D) 256

6.What is the volume of the cube (in cubic cm) whose diagonal measures 4√3 cm ?

(A) 8   (B) 16              (C) 27       (D) 64

7.If the length of radius of a right circular cylinder is doubled and height is halved, the lateral surface area will be

(A) equal         (B) double        (C) half            (D) 4 times

8.The length of a radius of a circle is 13 cm. and the length of a chord of the circle is 10 cm., the distance of the chord from the center of the circle is

(A) 12.5 cm.     (B) 12 cm.       (C) √69 cm.     (D) 24 cm.

9. The diagonals PR and QS of the rhombus intersect each other at the point O. What is the value of ∠POS?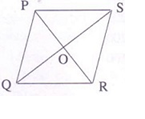

(A) Insufficient information      (B) 90°             (C) Any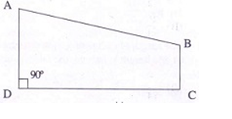 angle  (D) 45°

10.In the above figure AD | | BC, AD = 10 cm, BC = 5cm, CD = 10 cm. The area of ABCD is

(A) 150 sq.cm       (B) 75 sq.cm          (C) 500 sq.cm              (D) 250 sq.cm

11.A circular lawn has an area of 154 sq. meter. A path of 7 meter width surrounds the lawn. What is the area of the lawn including the path ? (in sq. meter)

(A) 580            (B) 516      (C) 616       (D) 637

12.A girl counted in the following way on the fingers of her left hand:

She started by calling the thumbs 1, the index finger 2, the middle finger 3, the ring finger 4, the little finger 5 and then reversed direction calling the ring finger 6, the middle finger 7 and so on. She counted upto 1770. She ended counting on which finger ?

(A) Thumb       (B) Index finger            (C) Middle finger      (D) Ring finger

13.A girl counted in the following way on the fingers of her left hand : She started by calling the thumb 1, the index finger 2, middle finger 3, ring finger 4, little finger 5 and then reversed direction calling the ring finger 6, middle finger 7 and so on. She counted upto 1994. She ended counting on which finger ?

(A) Thumb      (B) Index finger           (C) Middle finger          (D) Ring finger

1.How many metres of carpet 63 cm wide will be required to cover the floor of a room 14 m by 9 m ?

(A) 210 m        (B) 200 m       (C) 220 m         (D) 185 m

1.The area of a square field is 6050 m2. The length of its diagonal is

(A) 110 m        (B) 112 m        (C) 120m         (D) 135m

2.The area of a circle is 24.64 m2. The circumference of the circle is -

(A) 14.64 m     (B) 16.36 m         (C) 17.60 m             (D) 18.40 m

3.If the diagonals of a rhombus are 8 cm and 6 cm, the square of its side is -

(A) 25 cm2       (B) 24 cm2        (C) 55 cm2        (D) 36 cm2

1.The lenght of diagonal of a squire is 8 cm. The lenght of the side of the squire is

(A) 2.8 cm        (B) 1.414         (C) 2 cm        (D) 5.64 cm